Topology protocol walkthrough

This essay captures the second presentation given at Autonomous Anonymous 2024 in Lisbon. The video recording is available here. Special thanks to @goblinoats, @sylvechv, and @0xMugen_ for engaging discussions.

Prerequisite

A typical programmable blockchain operates a replicated state machine over an open peer-to-peer network. Nodes in the network collect user transactions against the state machine, and reach consensus on the total ordering of transactions periodically. The consensus process is able to tolerate Byzantine faults. Consensus is reached typically either through voting where votes are weighted by CPU power commmitted (Bitcoin) or by capital at stake (Ethereum, Tendermint).

This single-threaded operation for including and ordering transactions corresponds to the strict serializability consistency model. It is needed because the state of a smart contract is sensitive to the order at which transactions are executed against it. Coordination is required for total-ordering, and coordination is costly. Within Ethereum blocktime (~12 seconds), 99%+ is for reaching consensus.

Total-ordering all operations in a system is analagous to the concept of absolute spacetime. In Newtonian’s view of the universe, there exists a true time, which is independent to any observer. The true time progresses uniformly across the entire universe. Any occurrence in the universe is can be timestamped by this time. Therefore, any two occurences are comparable by this time.

Time is a tricky business in both physical and digital realities alike. Is it the ordering of events that defines the passage of time, or is it time that determines the ordering of events? Timekeeping is especially problematic in a distributed system where physical clocks can drift and where dishonest processes can report false physical timestamps. The use of private global networks and expensive equipment can almost get around the CAP theorem [1,2] but the solution is not tolerant to Byzantine faults. To sustain a notion of time as a total ordering of events and to tolerate Byzantine faults, Byzantine consensus algorithms are our best hope, but we are not satisfied here.

Given the cost of coordination (consensus), we wish to keep time without needing consensus. We wish for each process in a distributed system to be able to progress at their own speed, operate on shared stateful programs, and withstand Byzantine behavior. In other words, we wish to enable lock-free asynchrony with BFT. How is this possible?

It is possible: by changing the notion of time from total ordering to partial ordering of events. In a totally ordered set of events, any two events are comparable – event \(a\) either happened before event \(b\) (\(a \rightarrow b\), expressed with Lamport’s happened-before relation [3]) or happened after event \(b\) (\(b \rightarrow a\)). Partial ordering embraces the concept of concurrency. In a partially ordered set of events, any two events can be comparable or incomparable. When two events are incomparable (e.g. \(a \parallel b\)), in the context of timekeeping, we say they happened concurrently.

Intuitively, a system whose timekeeping embraces concurrency can operate with higher concurrency.

Now we are ready to restate our wish in terms of partial orders. We wish to avoid coordination but still ensure a notion of consistency: the processes in our distributed system can process operations, progress at their own speeds, and have the guarantee that they reach the same program state if they have processed the same partial-ordered set of operations.

A key insight is that there are many consistency models [4]. A typical blockchain operates on the strongest model of all: strict serializable consistency. To fulfill our wish, we want to choose the strongest possible model while staying away from coordination. That gives us … causal consistency! Under the causal consistency model, causal relations among operations are preserved across all processes.

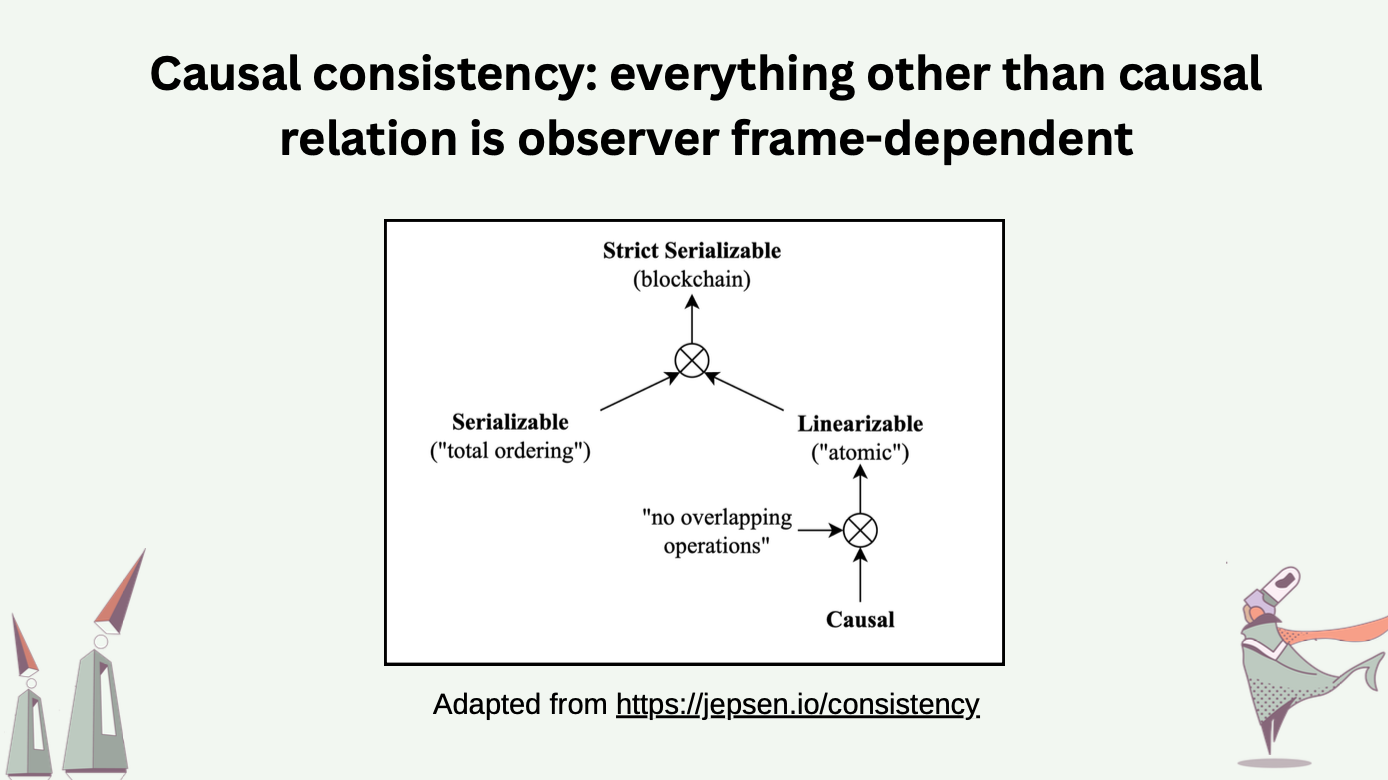
To understand what causal consistency means, we first need to understand what the causal relation is.

The causal relation among two events \(a\) and \(b\) takes three possible values (1) happened-before, denoted as \(\rightarrow\); (2) happened-after, denoted as \(\leftarrow\); (3) causally independent, denoted as \(\parallel\). If a process \(P\) generates event \(a\) then event \(b\), both by itself, we say \(a \rightarrow b\). If another process \(Q\) learns about event \(a\), and generates event \(c\) with such knowledge, we say \(a \rightarrow c\). These relations imply \(b \parallel c\), which means event \(b\) and \(c\) were concurrently generated and could not have causally depended on each other.

In a partial ordered set of events, where the partial order denotes the causality relation of \(\rightarrow\), the incomparable events are causally independent to one another.

Having covered the “causal part”, we now discuss the “consistency” part in causal consistency. For those events that are incomparable (concurrent), a process (assumed to be a single-threaded operation by distributed system convention) should be able to handle those events at arbitrary serialized order and still yield the same (or consistent) program state as every other process. Following our earlier example with \(a \rightarrow b\), \(a \rightarrow c\), and \(b \parallel c\), process \(P\) may execute these events in the serialized order \(a > b > c\), while process \(Q\) may execute these events in the serialized order \(a > c > b\). Effectively, the serialized histories of events seen by process \(P\) and \(Q\) are different, but they should yield the same outcome (convergence): they continue to stay in and interact with the “same universe”.

CRDTs are data types that exhibit the properties described above. They allow concurrent operations to be performed in arbitrary order and guarantee state consistency.

Shifting from total ordering to partial ordering constitutes a mental shift that gives up the existence of true time and reliance on it. From special relativity we know that it is nonsense to ask about one’s time without knowing one’s observer frame. In Einstein’s thought experiment about trains and light, two light beams emitted from the center of the train carriage in opposite directions should reach the ends of the carriage simultaneously for observers on the train, but not for observers standing on the railroad embankment. In other words, the ordering of events is relative to observer frames, while all observers do observe the same universe.

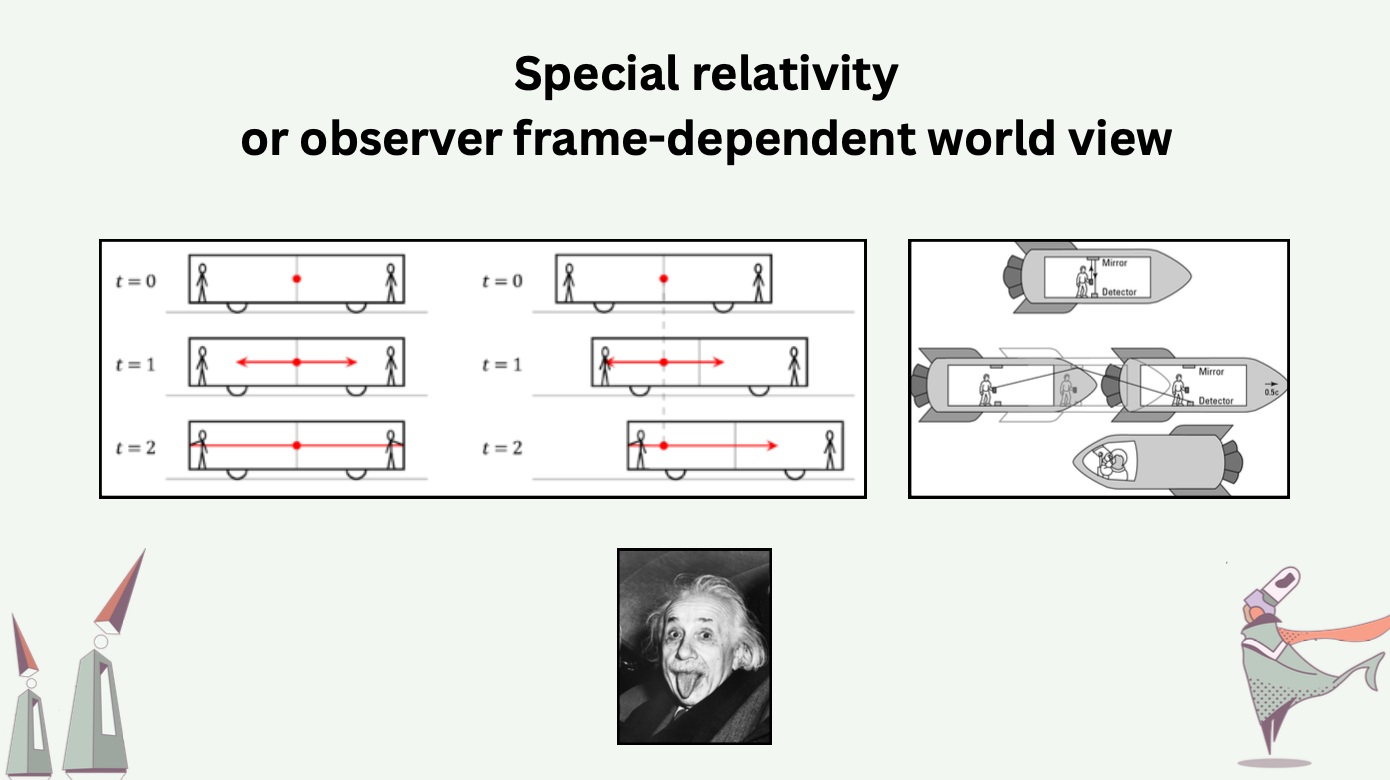
The last piece of the prerequisite is concerned with Byzantine behaviors. Following our earlier example, if process \(P\) tells process \(Q\) about event \(a\), event \(b\), and their relations \(a \rightarrow b\), how can \(Q\) trust that \(P\) is not lying? We can follow the old wisdom of hash links and cryptographic signatures to construct a self-certifying hash graph which records the partial ordering among events [5].

Putting these building blocks together, we can restate our wish one last time. We wish to construct causally-consistent CRDT programs that are BFT by having their events transported in self-certifying DAGs called hash graphs. These programs can execute in a distributed and lock-free manner on open peer-to-peer networks and tolerate Byzantine actors. An additional wish is that these programs should interact among themselves also in a lock-free manner i.e. message-passing.

Overview of protocol stack

We adopt the layered architecture tradition and conceptualize our protocol stack in layers with segregated responsibilities. On the bottom of our protocol stack lies the peer-to-peer messaging layer, which sits on top of the Internet’s TCP/IP layer. The peer-to-peer messaging layer includes protocols for transferring messages one-to-one and one-to-many in the peer-to-peer manner. We aim to leverage libp2p as much as possible at this layer.

On top of the peer-to-peer messaging layer is the causal consistency layer (alternatively, hash graph layer), which is responsible for the synchronization and reconciliation of hash graph replicas among peers.

On top of the hash graph layer, we can construct CRDTs and live objects. Live object layer specifies the protocol for spawning and synchronizing live objects, as well as for live objects to signal one another.

Also on top of the hash graph layer, we can construct a DAG-based consensus mechanism that uses the threshold logical clock primitive for pace-making [6]. This mechanism spans two layers: a threshold witness layer, and on its top, a consensus layer.

On top of the consensus layer is the RAM layer, which leverages consensus on hash graphs to operate snapshot, compaction, and coherence protocols for live objects.

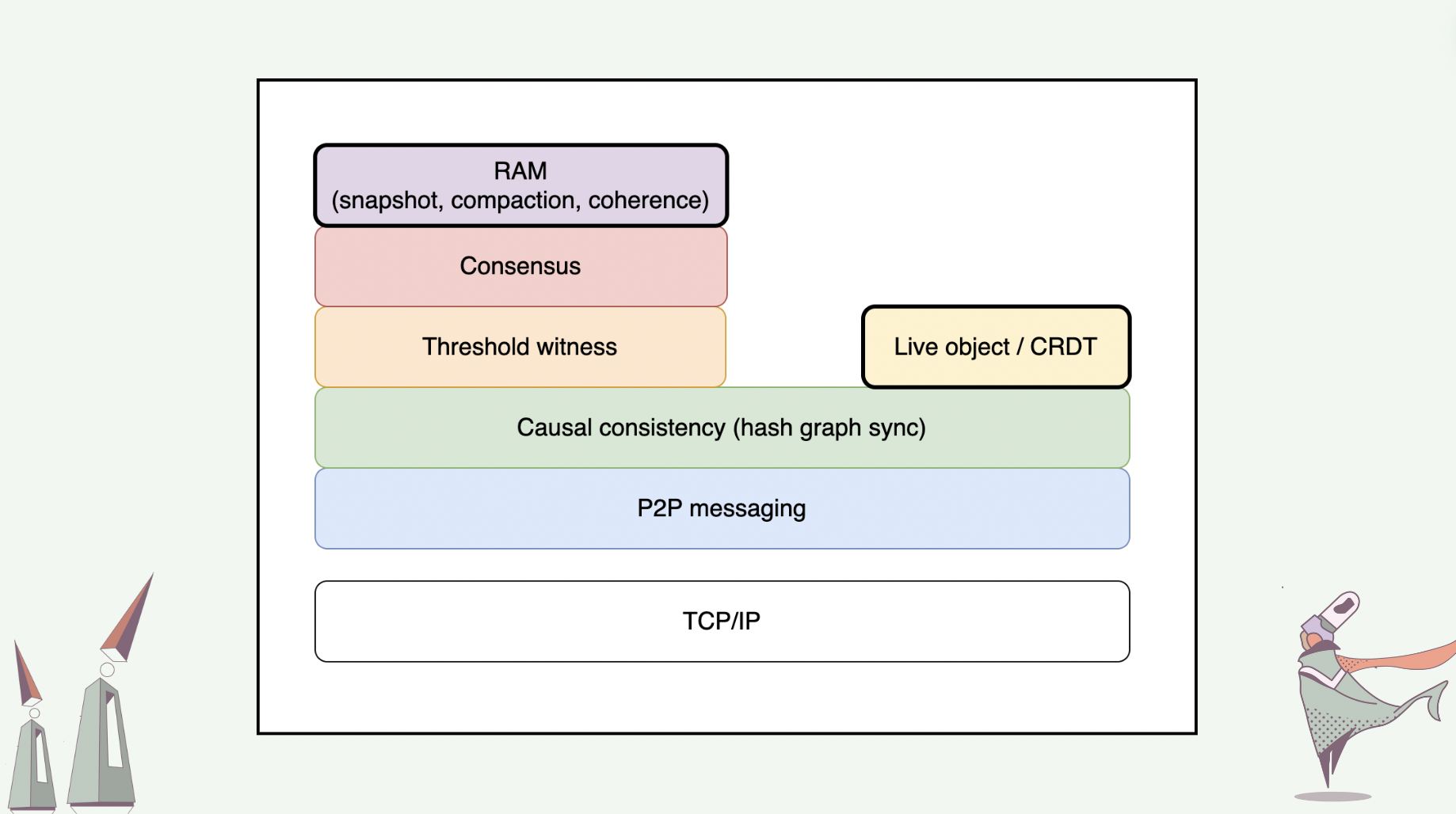
In this talk, I will only cover hash graphs, CRDTs / live objects, and some intuitions behind the RAM layer.

Hash graphs

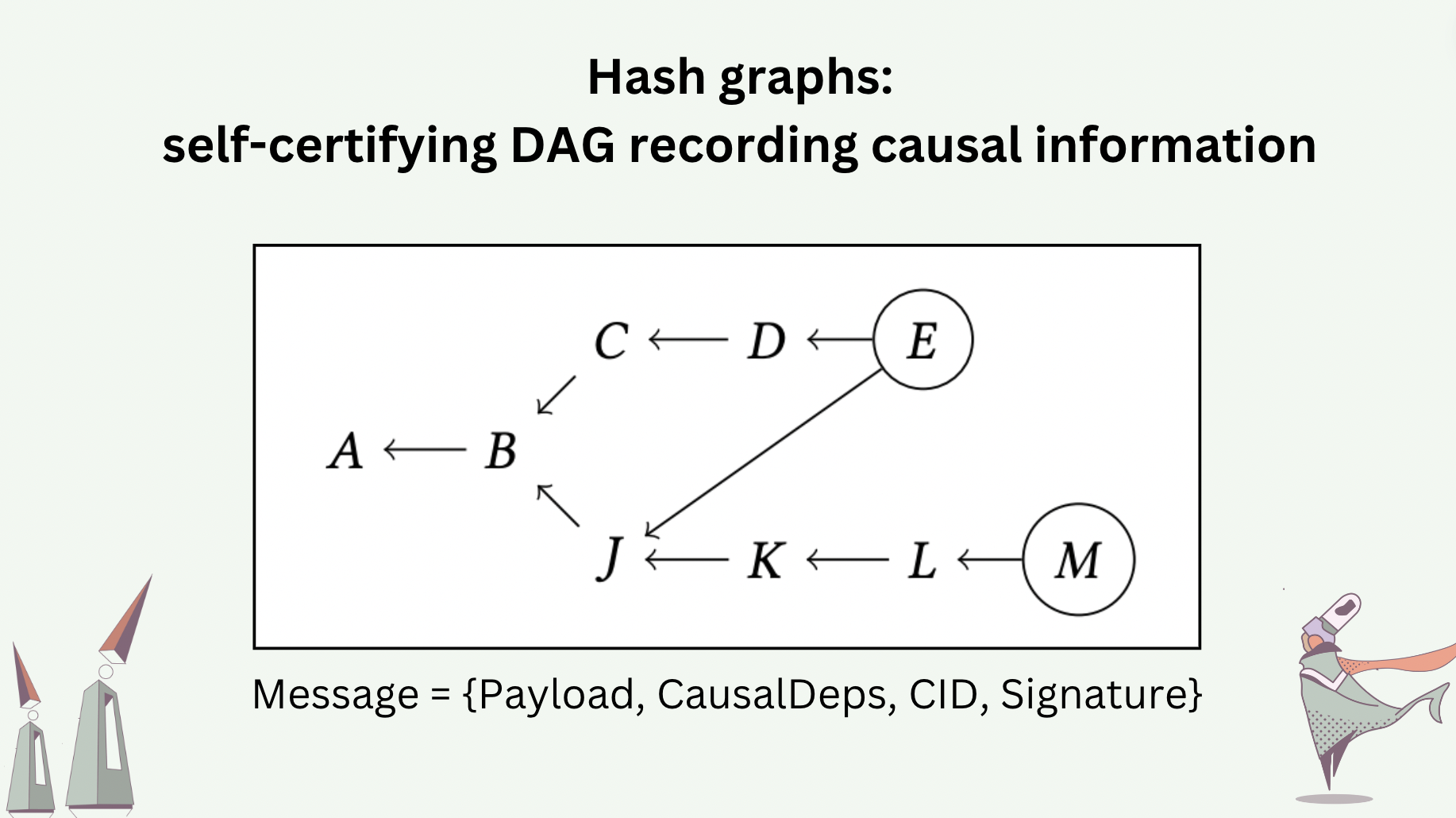
To make causal relations tamper-proof, we use hash graphs to transport the history of a program executed in a distributed manner. A hash graph is a DAG whose nodes are messages and whose edges are causal dependencies reported by the messages. Each message takes the basic structure \(\{Payload, CausalDependencies, CID, CryptographicSignature\}\). The \(CID\) (content identifier) uniquely identifies the combination of \(Payload\) and \(CausalDependencies\). The cryptographic signature uniquely identifies the process that generates the message, who signs the \(CID\) with their private key.

Every process in our distributed system maintains a hash graph replica.

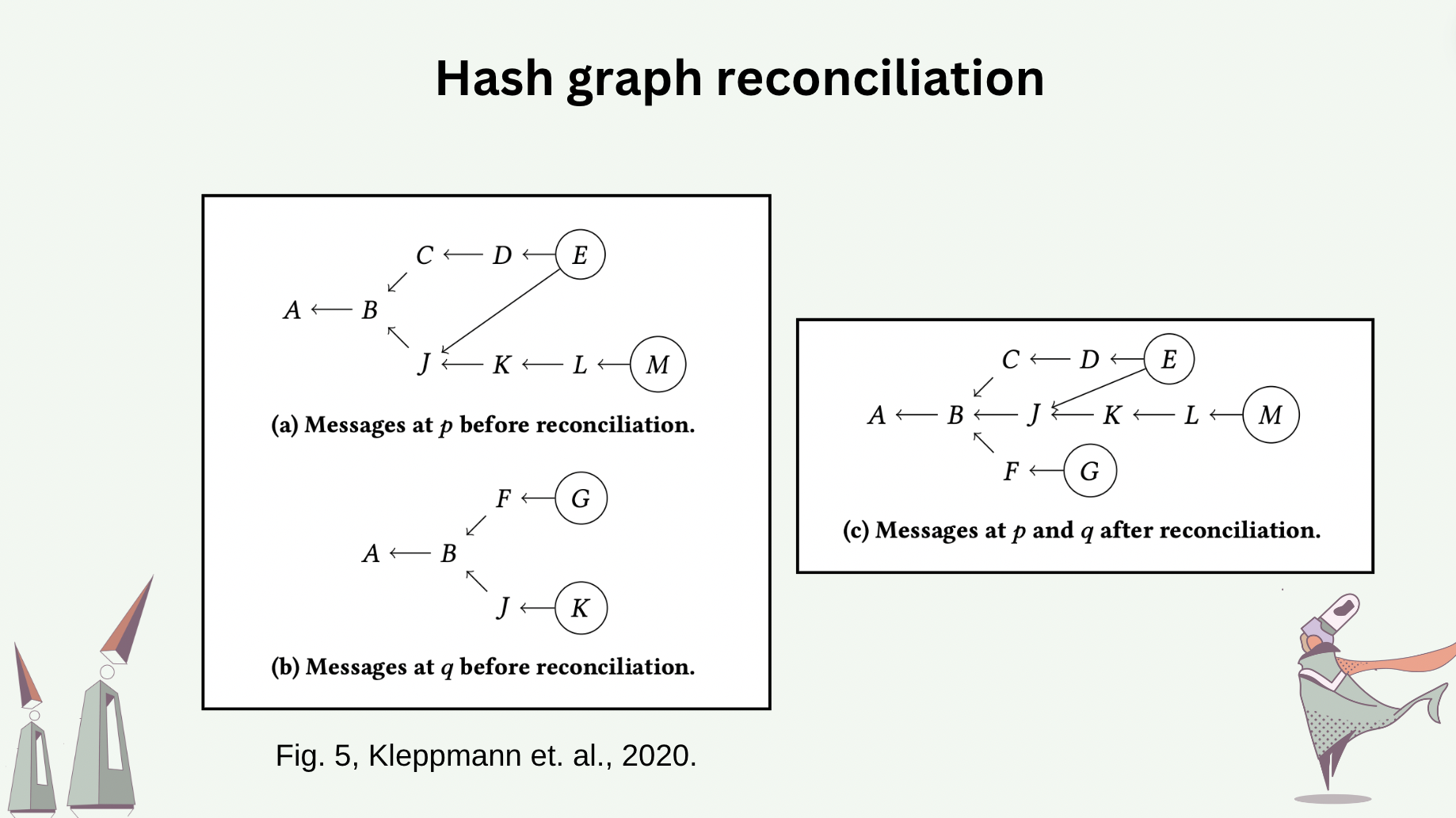
The parent-less messages in a hash graph (i.e. root nodes in the DAG) are called “heads”. Heads are the latest messages added to the history. The slide shows an example of a hash graph, where the heads \(E\) and \(M\) are encircled. We require every new message, to be added to a hash graph, to report the heads of the hash graph as its causal dependencies (more precisely, the CIDs of the heads).

The number of heads indicates the degree of concurrency in the system. Consider a system, where processes perform operations periodically at an interval that is significantly longer than the network delay between the processes. It is easy to imagine that the hash graphs of these processes would rarely have more than one head each at a time.

Consider a hypothetical two-player game whose events are transported by a hash graph. Each player operates at 60 Hz (i.e. each player adds a new message to their hash graph 60 times a second). Assume there is a 30-milisecond network delay (one-way) between the two players. The hash graphs at player \(A\), immediately before and after adding message \(A_5\), would look like the following.

The differences between hash graphs of the processes can be reconciled. Synchronizing two hash graphs is equivalent to reconciling their differences. Note that a message whose causality can not be recognized locally will be rejected. An “effect” is accepted by a process if the effect’s causes can be traced to one of the messages already in the process’s hash graph. The following slide shows the hash graphs before and after process \(p\) and \(q\) reconcile between themselves.

Hash graph-transported CRDT

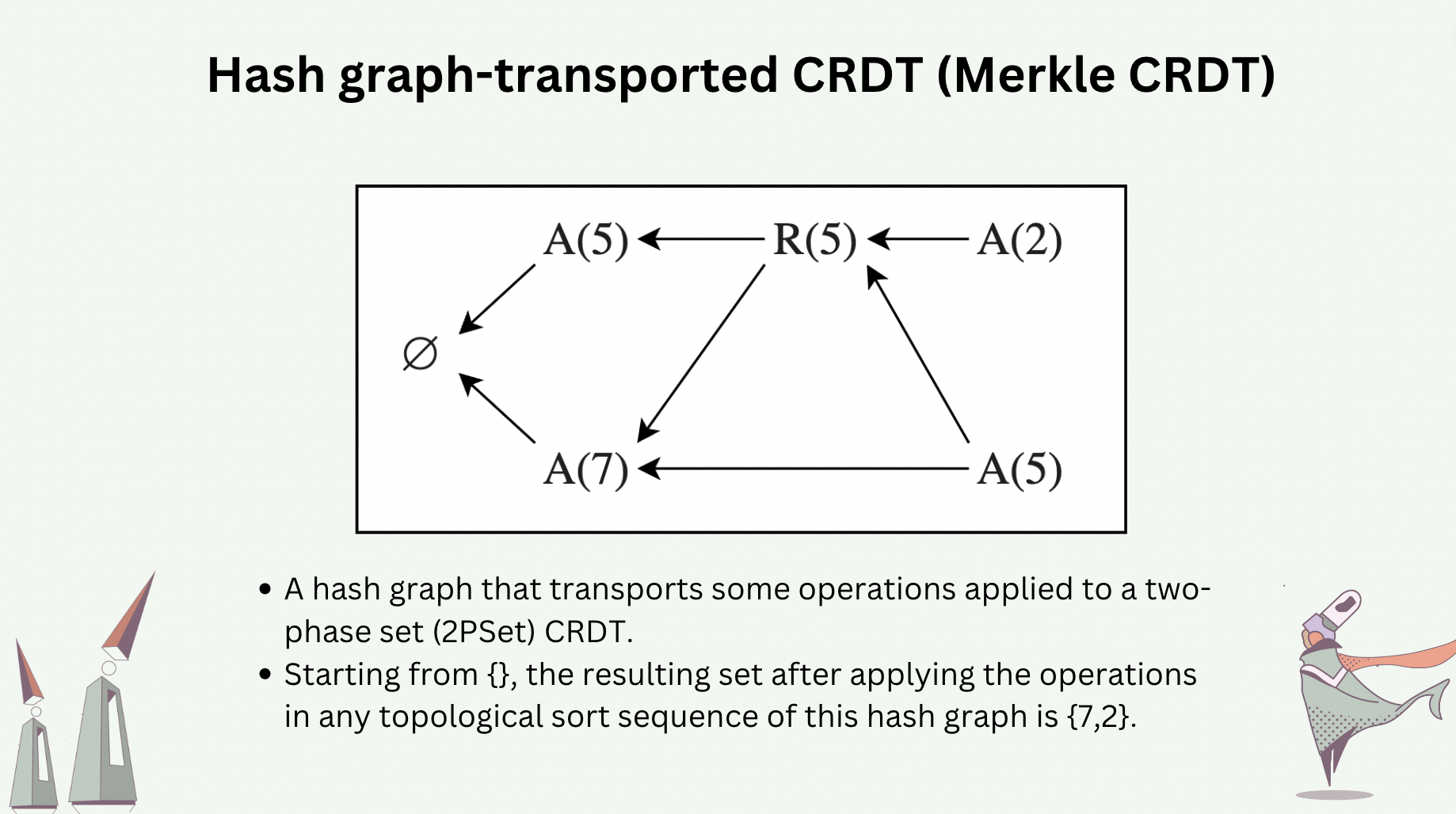
Operations or deltas of a CRDT can be transported by a hash graph [7,8,9], making such a CRDT tolerant to Byzantine faults.

The following slide shows some operations of a two-phase set CRDT that are transported in a hash graph. Executing the operations sequentially, by any valid topological sort sequence of this hash graph, would yield the same CRDT state.

Live objects

Intuitively, live objects are Smalltalk-like objects (actors) made with CRDTs [10].

Each live object is an instance of a blueprint (class), whose states are typed with built-in CRDTs or other blueprints. This means live object blueprints are composable and that each live object is a compound CRDT.

Live objects interact with the outside world by signaling (asynchronous message-passing). Signals are typed and reified. A live object’s interface specifies the set of signal types the object handles.

Each state-mutating signal handler is a monotonic function. A monotonic function is an inflation, which means it only adds information to the state and never removes information.

Each blueprint specifies one or multiple view function, which returns a serialized state of the live object.

Each blueprint also specifies a commutative merge function for merging two replicas of the same live object.

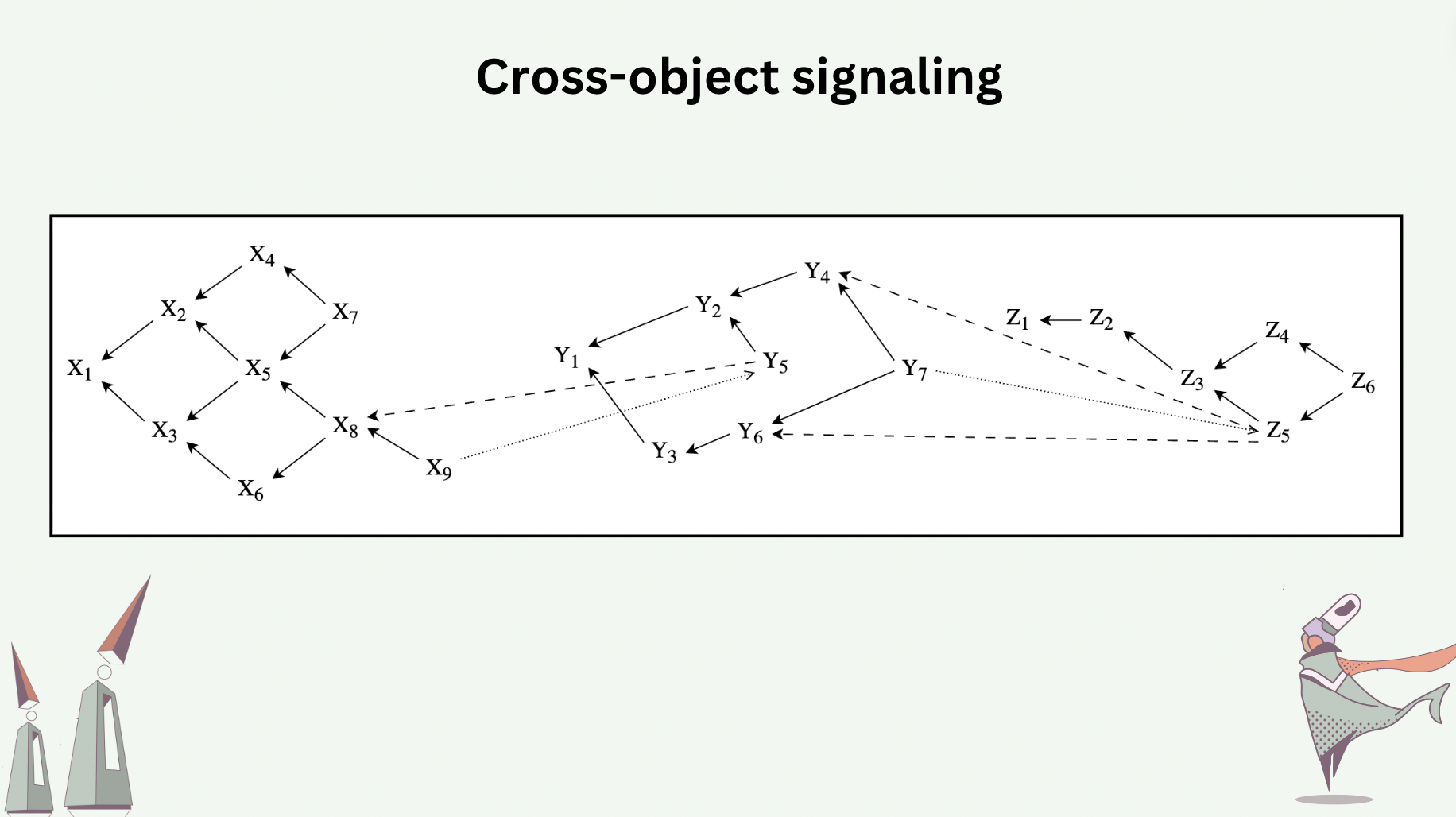
Live objects can signal one another, called Cross-Object Signaling (COS). COS reports causal dependencies both in the hash graph of the sender object and in that of the receiver object.

Random access memory

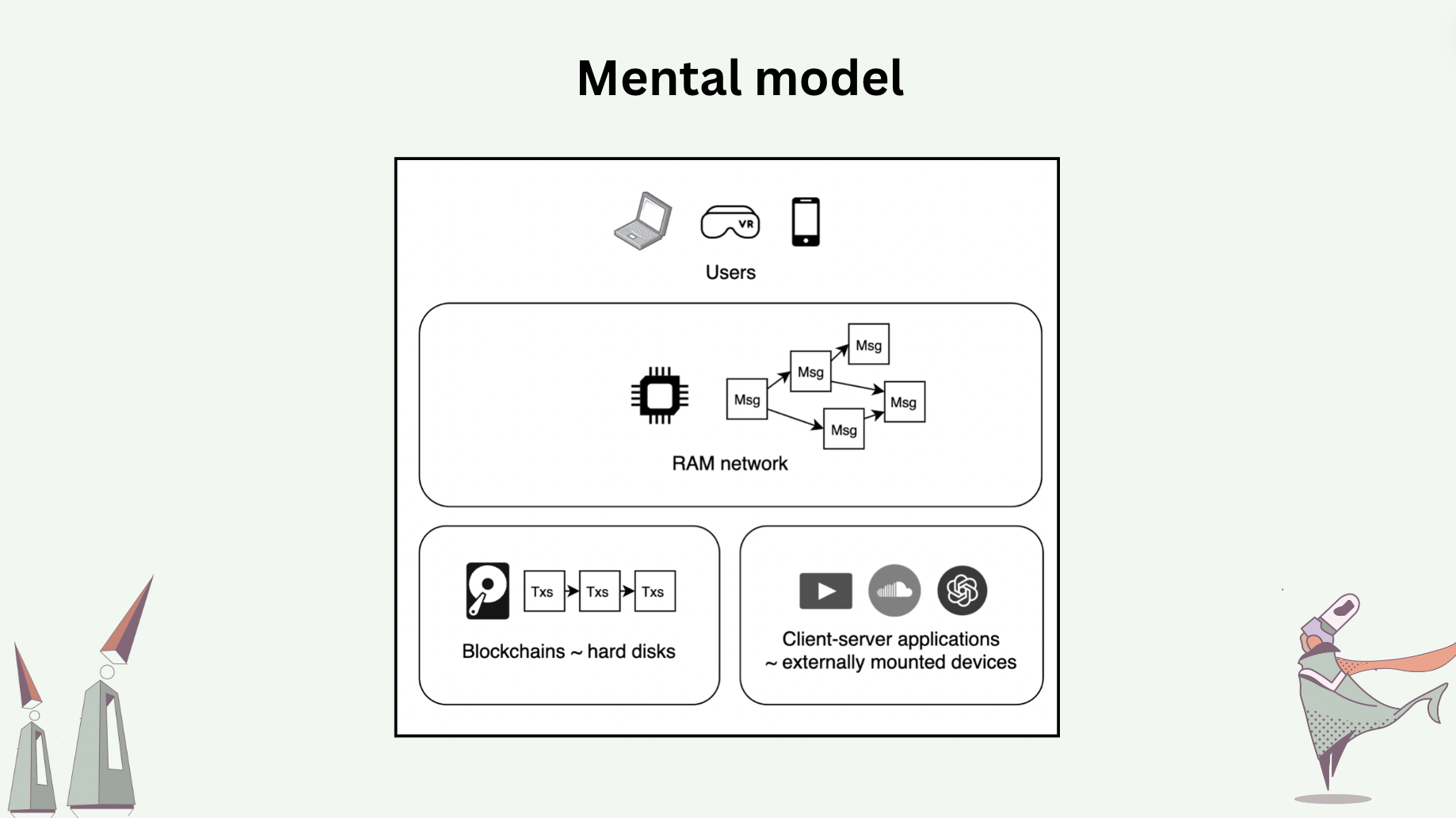
Now we move on to the “RAM” concept. The role of random access memories in computers is to serve as intermediary memories, or buffers, between CPUs and main memories, which have long access time. The main memory may have a 1ms access time, while the RAM may have a 1ns access time. Despite having lower memory density, their physical closeness to CPU and much shorter access time make them the ideal buffers for data that is being or will be frequently accessed. Coming back to the world computer, our view of the status quo is that blockchains are analogous to hard disks whose reads/writes are serialized, whose writes are expensive (users are paying for consensus), and whose access times are long (users must wait for consensus before sending subsequent transactions). This means that onchain decentralized applications today run directly on the hard disks of a world computer. Additionally, most blockchain users rely on centralized gateways, instead of joining the underlying peer-to-peer networks as peers, to access smart contracts on blockchains – ironically, blockchains are peer-to-peer, but most users operate in the client-server fashion, making themselves vulnerable to congestions at these gateways as well as additional trust assumptions [11].

The modular thesis of blockchain scaling is essentially proposing to “stack hard disks on top of hard disks”, which hardly feels like a solution to the fundamental problems.

Our proposal is to introduce “random access memory” to the world computer, which is a peer-to-peer network that operates live object replicas. Every user of live objects runs a peer of this RAM network locally themself, which allows them to interact with live objects in a local-first fashion. User peers operate the replicas of only live objects of interest. On the contrary, blockchain full nodes must synchronize on the full serialized history of the entire universe of smart contracts, making them prohibitive for regular users to operate locally.

To sustain the local-first access patterns, it is important that (1) live object histories are kept succinct, and (2) inactive live objects are ejected from the RAM network until users wish to access (replicate) them. Succinctness requires periodic snapshot and compaction of the hash graphs of live objects. Ejection and bring-back (“rehydrate”) requires a coherence protocol, not unlike those for multiprocessor systems, that also involves snapshotting.

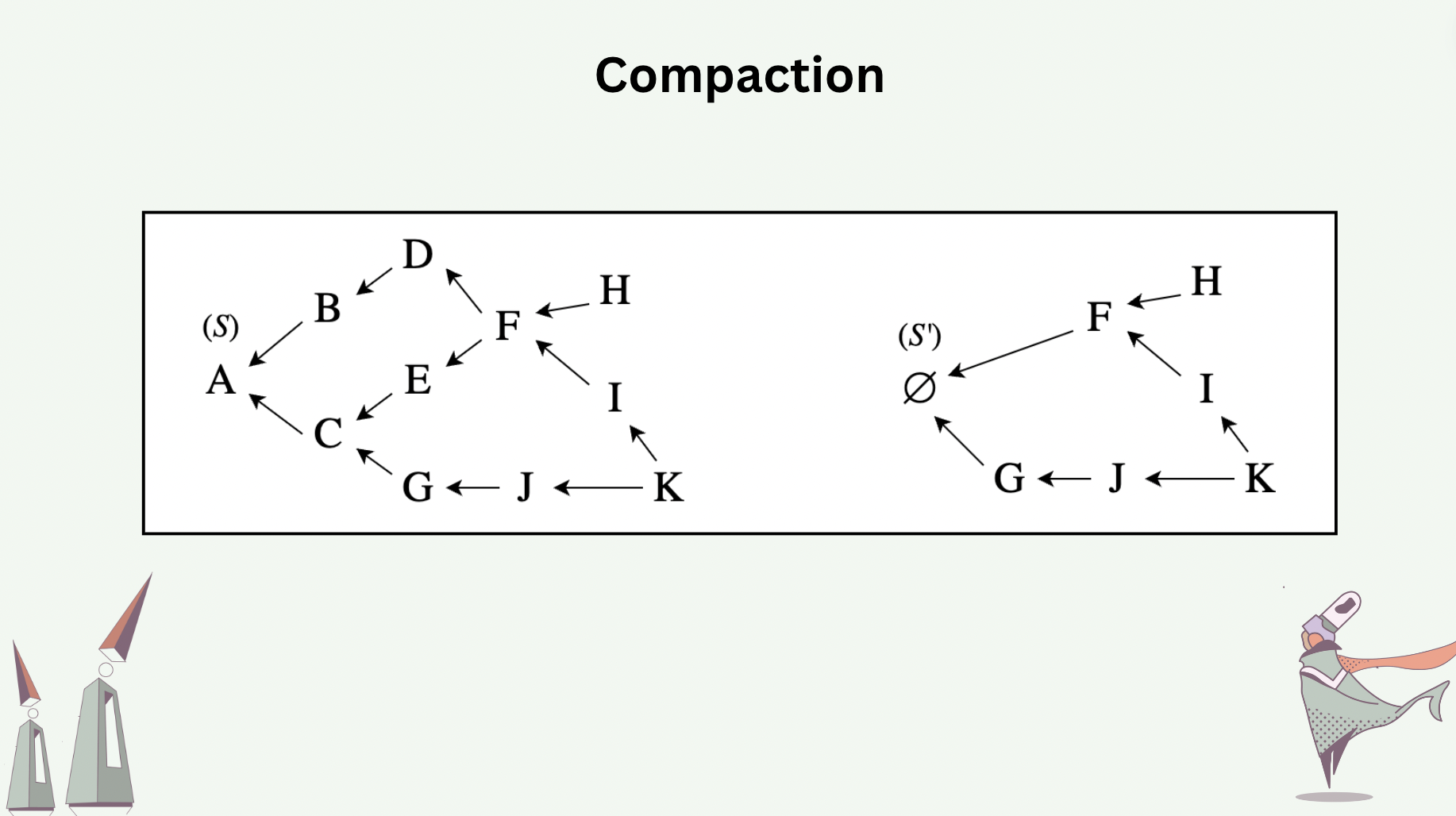
Compaction throws away causal information in a hash graph, and reclaims memory space in return.

Compaction is perfectly safe only when performed over stable messages. Stable messages are messages in a hash graph with the guarantee that all future messages to be added will have happened after them. The following slide shows the how messages \(A,B,C,D,E\) are compacted away, assuming messages \(F,G\) are stable. Compaction also involves state advancement. In the slide, the new tail message \(\emptyset\) carries with it a state \(S'\), which is obtained by executing the payloads (CRDT operations or deltas) of the compacted messages in a valid topological sort sequence over the previous state \(S\).

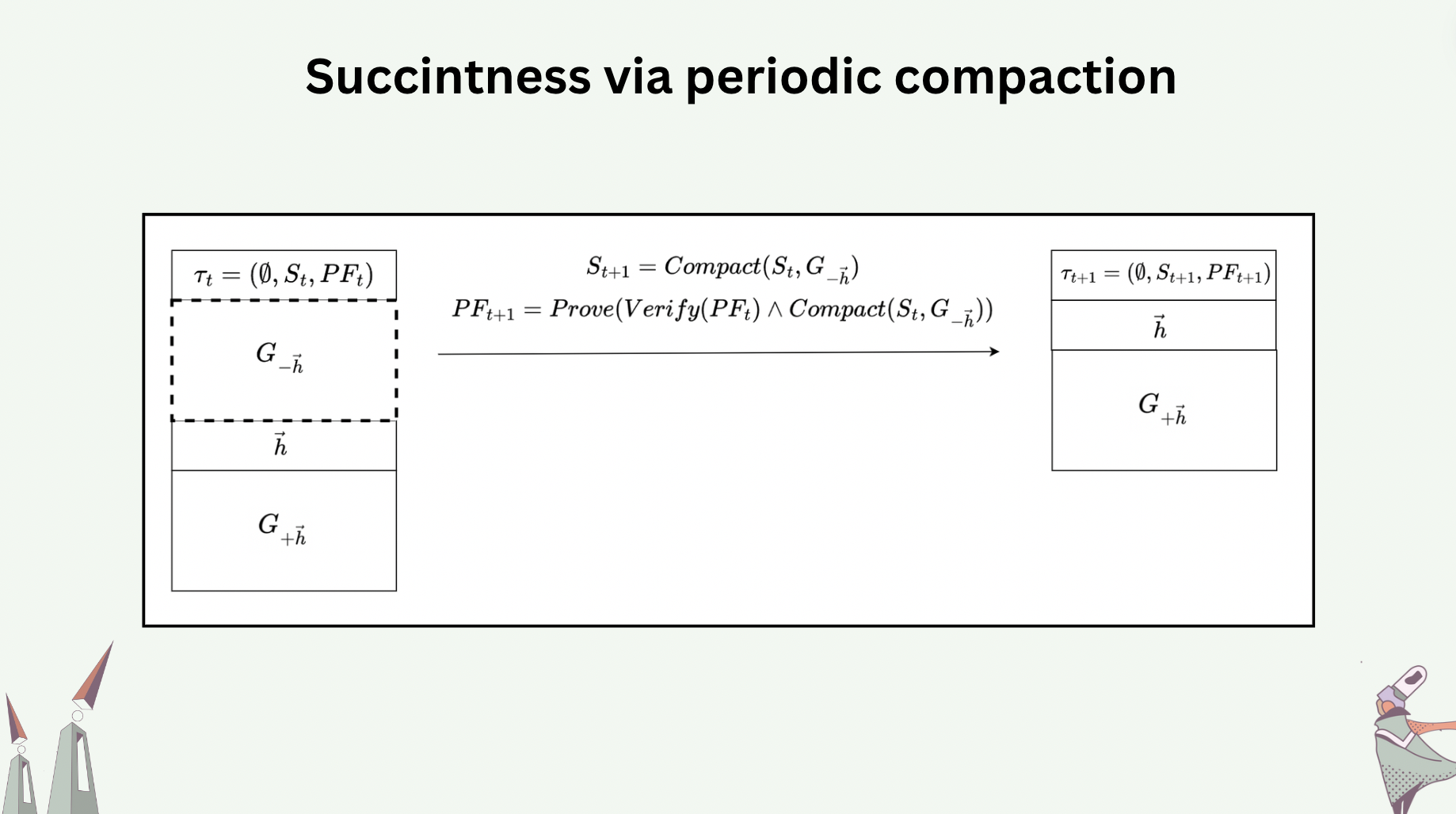
To have succinctness that is also verifiable, we require the compaction (state serialization) to be validity-proven. In fact, a proof of compaction is a recursive proof: it includes proving the compaction itself as well as proving the verification of the proof of the last compaction run.

Security problems

We foresee plenty of security problems that need to be dealt with. Here we discuss two of them.

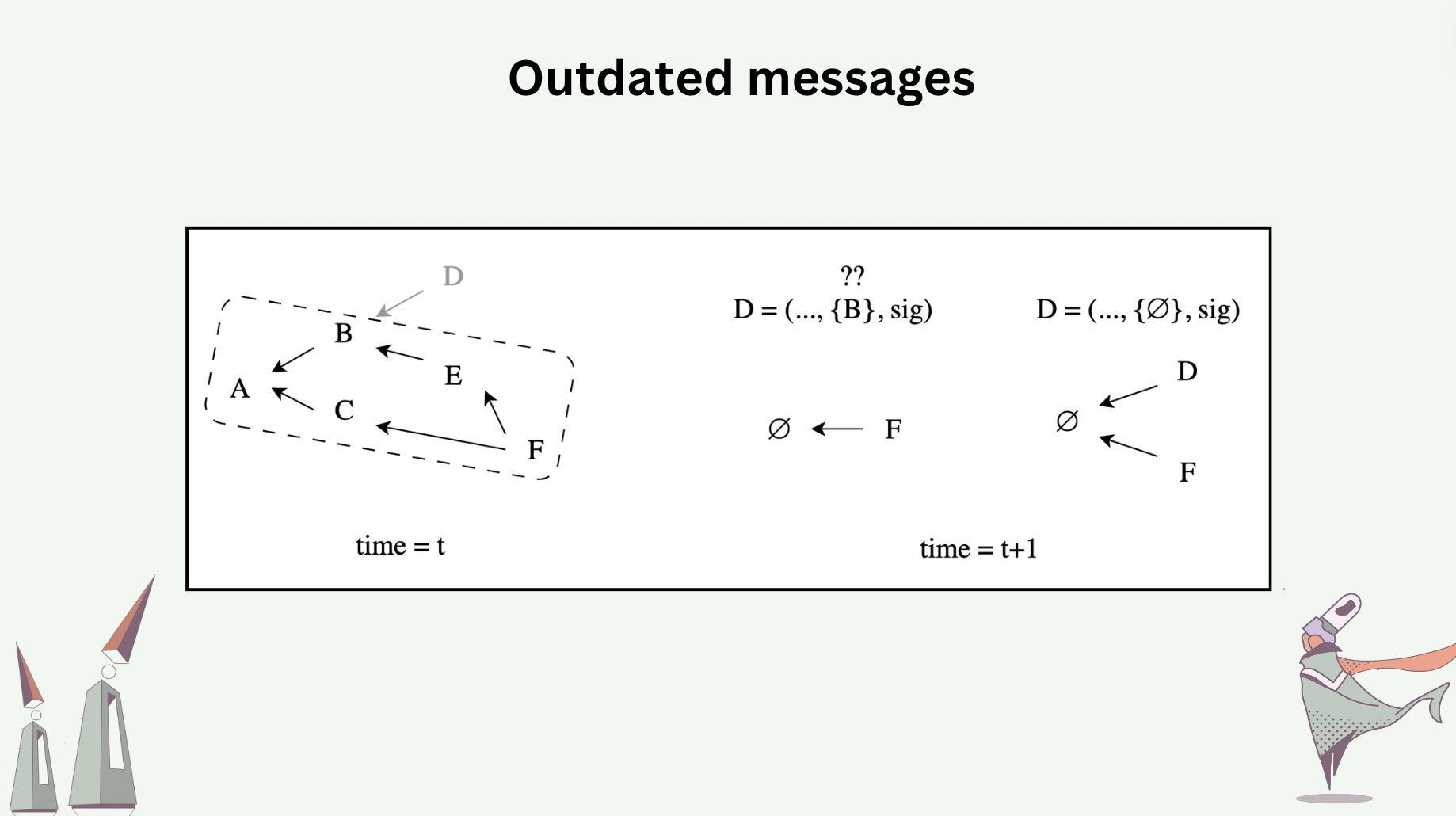
Outdated messages are messages with causal information unrecognized by a hash graph, due to unsafe compaction. In the following slide, messages \(A,B,C,E\) were compacted away before message \(D\) arrives, which causally depends on \(B\). From the perspective of the compacted hash graph, there are two interpretations of message \(D\)’s unrecognized causal dependency: \(D\) either arrives too late, or \(D\) was generated by Byzantine actor who reported nonexistent causal dependency.

If \(D\) simply arrives too late, consider reconstructing \(D\) by resetting its causal dependency to either the tail message or the heads. Can the reconstructed \(D\) be added to the hash graph? Notice that the original signature that came with \(D\) is no longer valid in the reconstructed version. Who needs to sign the reconstructed version? Consider two processes \(P\) and \(Q\), both encountering the scenario above, and both attempting to reconstruct \(D\). If both processes sign the reconstructed version with their own private key, they ended up adding different variations of \(D\) to their graph.

Analyzing the security and performance implications of outdated messages, as well as how to differentiate between those that arrive too late from those that were Byzantine, are open research problems.

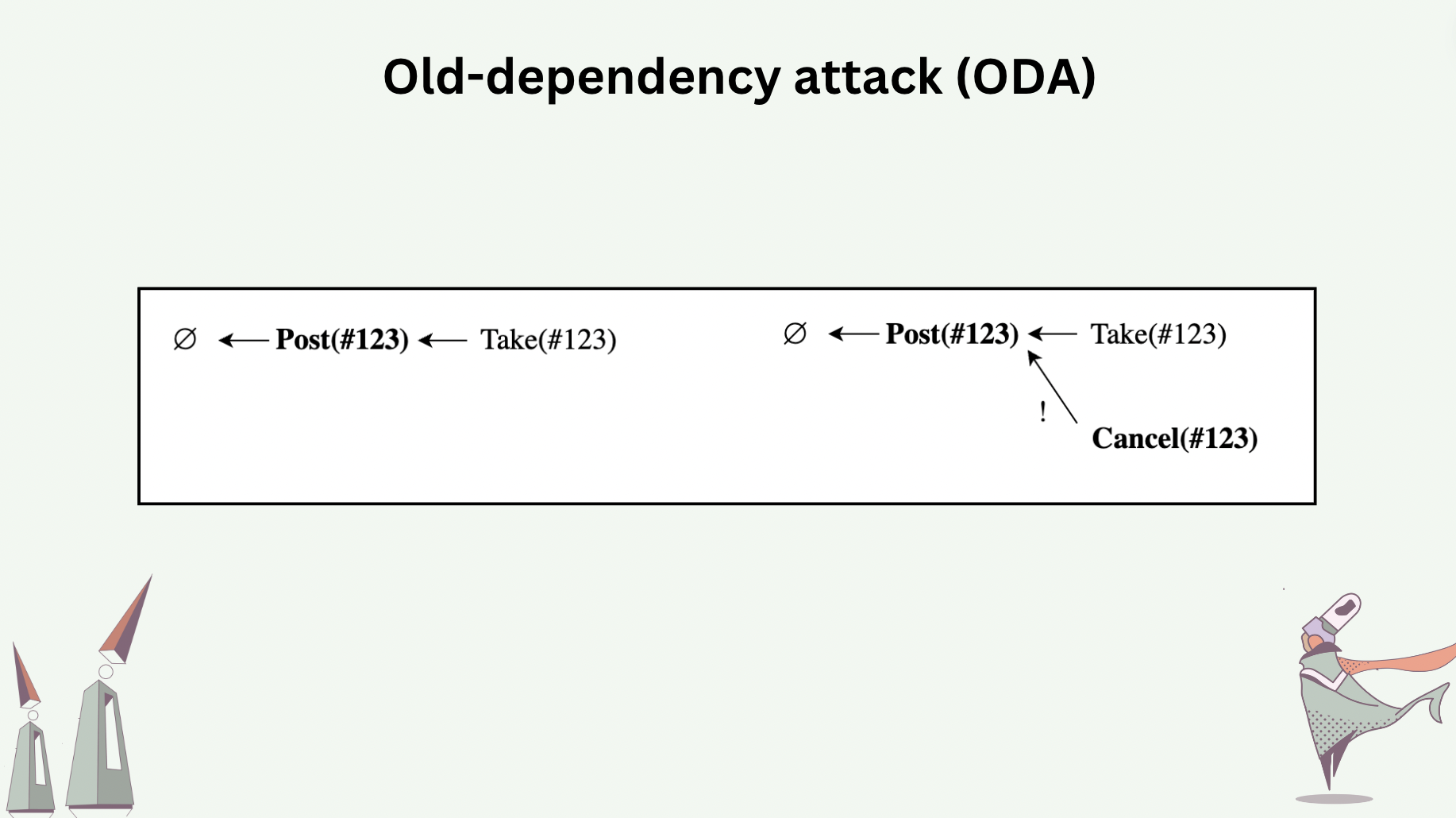
Old-dependency attack (ODA) is an attack where messages report old dependencies instead of the heads of the graph at the time of message generation.

The following slide shows a hypothetical live object that implements a decentralized exchange as CRDT, which has three operation types: Post, Take, and Cancel. The DEX requires that (1) only the process that generated a Post can Cancel that Post, and (2) if a Cancel is concurrent to a Take, Cancel wins.

ODA occurs when the process which posted an order sees a Take and decides to “regret” by sending a Cancel. This Cancel incorrectly reports the Post as causal dependency as opposed to the current head which is the Take. As a result, the Cancel appear to be concurrent to the Take, therefore invalidating the Take.

How to discourage, mitigate, detect, reject, and recover from such attack is an open research problem.

Mental models

Some mental models that we operate on are:

1. Essentially, the RAM network operates a Smalltalk-like system where objects are replicated and synchronized without coordination. All communication is peer-to-peer.

2. The decentralized applications of the future will have two backends: one set of smart contracts, and one set of live objects.

3. Live objects complement the strength (e.g. strict serializability) and weakness of smart contracts. Together they allow us to build larger and more useful hyperstructures.

Project status

Prototyping effort is open sourced at this repo.

We are currently tackling research problems around snapshot, compaction, coherence, consensus algorithms and security problems. Meetings notes from weekly collaborator calls can be found in this repo.

We are looking for research engineers to join us. More information to be shared soon.

Expect regular public dev calls and blogposts for updates and discussions.

Reference

[1] Corbett et. al., Spanner: Google’s Globally Distributed Database, 2013. link

[2] Brewer, Spanner, TrueTime & The CAP Theorem, 2017. link

[3] Lamport, Time, Clocks, and the Ordering of Events in a Distributed System, 1978. link

[4] Jepsen’s map of consistency models. link

[5] Kleppmann et. al., Byzantine Eventual Consistency and the Fundamental Limits of Peer-to-Peer Databases, 2020. link

[6] Ford, Threshold Logical Clocks for Asynchronous Distributed Coordination and Consensus, 2019. link

[7] Sanjuán et. al., Merkle-CRDTs – Merkle-DAGs meet CRDTs, 2020. link

[8] Kleppmann et. al., Making CRDTs Byzantine Fault Tolerant, 2022. link

[9] Almeida et. al., The Blocklace: A Universal, Byzantine Fault-Tolerant, Conflict-free Replicated Data Type, 2024. link

[10] Goldberg et. al., Smalltalk-80: the Language and its Implementation, 1983. link

[11] Marlinspike, My first impressions of web3, 2022. link